Ecuacion Traslacional:
Un cuerpo rígido lleva movimiento de Traslación cuando todo
segmento rectilíneo del cuerpo se mantenga paralelo a su posición inicial a lo
largo del movimiento.
Durante la Traslación, no hay movimiento angular (ω = α = 0); por tanto, todas las partes del
cuerpo tienen la misma aceleración lineal a.
La Traslación sólo puede tener lugar cuando la recta soporte
de la resultante de las fuerzas exteriores que se ejercen sobre el cuerpo pase
por su cdm G.
En el caso de Traslación, con el origen del sistema de
coordenadas xyz en el cdm G del cuerpo, las ecuaciones para un movimiento plano
cualquiera se reducen a:
Ejemplo:
Calcula el
momento angular de la Tierra respecto al centro del Sol, despreciando el movimiento de rotación de la Tierra sobre si
misma y considerando a la ́orbita de la Tierra como circular. Datos: MT= 6·1024kg; r orbita= 1, 5·108km
Solucion:
La velocidad de traslación de la Tierra alrededor del Sol
es:
Considerando
a la Tierra y al Sol como objetos puntuales y suponiendo que la orbita de la
Tierra es circular alrededor del Sol, entonces el vector de posición y el
vector velocidad de la Tierra respecto al Sol son siempre perpendiculares. Por
tanto, el momento angular de la Tierra respecto del Sol es un vector
perpendicular al plano de la ́orbita del planeta, cuyo modulo es:
Ecuacion Rotacional:
Este tipo de movimiento plano se produce cuando todos los
elementos de un cuerpo describen trayectorias circulares alrededor de un eje
fijo. La figura representa un cuerpo
rígido simétrico respecto al plano de movimiento, y que gira en tomo a un eje fijo que pasa por el cdm G del cuerpo:
Ejemplo:
Determine la inercia rotacional de una varilla de 4 m de largo y 2 Kg de mesa si su eje de rotación es:
a) Un extremo de la varilla
b) El centro de la varilla
a) Un extremo de la varilla
b) El centro de la varilla
Solución:
a) Si el eje de rotación es un extremo de la varilla, la inercia rotacional está dada por I = 1 /3 ML2
- Remplazando los valores, se tiene:
b) Si el eje de rotación es el centro de la varilla, entonces, ahora se tiene que I = 1 /12 ML2
- Remplazando los valores, se tiene:
Ecuación de Plano General:
Para esta ecuacion podemos visualizar un cuerpo rigido como se presenta en
la siguiente imagen en donde es sometido a un plano general, podemos asociar
las ecuaciones anteriores, el cual determinamos que las ecuaciones que
representan el plano general es la siguiente manera:

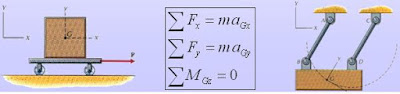





No hay comentarios:
Publicar un comentario